Anshul Jain
23 Apr 2020
In recent years, Artificial Intelligence (AI) has had a tremendous impact on the technologies of robotics, pathfinding, and problem-solving. Moreover, Humans are dependent on these technologies to find solutions and perform tasks. However, what makes these actions possible? The answer is simple: Search Algorithms. Searching is an integral part of AI, and AI machines use it, along with various search algorithms techniques to systematically explore alternatives and find the most suitable path to reach the goal.
That’s not all, these search algorithms are divided into two major parts Uninformed and Informed Search Algorithms, which make this search more streamlined and accurate. It is one of these types- the Uninformed Search Algorithm -that we are going to discuss in detail today, along with various uninformed search strategies.
What is Uninformed Search?
Based on the available information about the problem, the Search Algorithm is first categorized into Uninformed Search Algorithm, which generates the search tree without any domain-specific knowledge or additional information about the states beyond the information provided in the problem definitions. This class-purpose search algorithm, which is also known as Blind Search or Brute-Force Search, operates in a brute-force way and examines each root node of the search tree until it achieves the goal state.
It works effectively with small possible states and can be applied to a variety of search problems, as it does not take into consideration the target problem and is only registers it once it achieves the final goal. Moreover, the uninformed search includes six (6) search strategies, which are obtained on the basis of the selection path implemented in the frontier.
But, before we move on to answer “what is uninformed strategy?”, we need to understand the requirements of the Uninformed Search Algorithm and the various components covered by its search strategy.
Requirements of Uninformed Search:
Though Uninformed Search does not require excessive details about the problem, it does have a few search requirements, like:
- State Description:States that are reachable from the initial state by any sequence of actions as well as details like where the search begins, ends, transition model, etc.
- A valid set of Operations: That helps find the most optimal solution with the lowest cost.
- Initial State:Information about the stage where the agent first starts the search.
- Goal State Description:Details like the limit of the search tree, the sequence of nodes from start to goal, etc. should be considered.
Components Included in Uninformed Search:
In Uninformed Search Algorithms, each of the six search strategies covers the following components, which becomes helpful at a different stage of problem-solving. These components are:
- Problem Graph: Contains the start and goal nodes.
- Strategy: Describes the manner in which the graph will get to the goal.
- Fringe: Includes the data structure used to store all the possible states that can be achieved from the current state.
- Tree: It is the result of traversing from the start node to the goal node.
- Solution Plan: This is the sequence of nodes from the start to the goal node.
Now that we understand the basics of Uninformed Search Techniques, we can move on to discussing the various strategies of Uninformed Search.
What Are the Various Uninformed Search Techniques?
Uniformed Search Techniques are various goal-achieving strategies that don’t take into account the location of the goal, as they are not focused on the path of reaching the goal until they find it and report success. These strategies are of sic (6) types:
1.) Breadth-First Search:
The most common search strategy, breadth-first search, starts from the root node, explores the neighboring nodes first and moves towards the next level. Implemented using the First-in First-out (FIFO) queue data structure, this is an example of a general-graph search algorithm that provides the shortest path to the solution.
Moreover, it is useful in the following conditions:
- When the problem is small enough and space complexity is not a problem.
- you want a solution containing the fewest arcs.
Example:
Consider the following graph, where the BFS algorithm traverses from A to B to E to F first then to C and G lastly to D to reach the goal state.
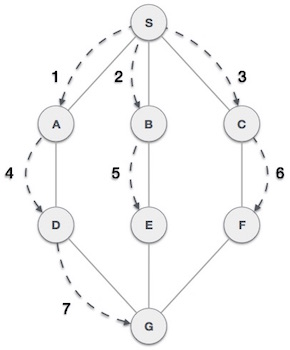
In this graph, the algorithm uses a queue to remember to get the next vertex to start a search as well as when a dead end occurs in any iteration. Without this queue, it won’t be able to identify and mark visited vertices and will process them again, which can then become a non-terminating process.
In short, breadth-first search or BFS expands the shallowest node, with the lowest depth, first.
2.) Depth-First Search:
Implemented using the Last in, First out (LIFO) stack data structure, Depth-first Search or DFS is used to traversing tree or graph data structures. This algorithm expands the deepest node and is like the breadth-first search. But unlike the latter, it starts from the root node and follows each path to its greatest depth before moving to the next path or backtracking.Moreover, DFS improves memory requirements by deleting the entire line once it is explored and requires less memory, as it only needs to store a stack of the nodes on the path. Also, it takes less time to reach the goal node than the BFS algorithm.
Example:
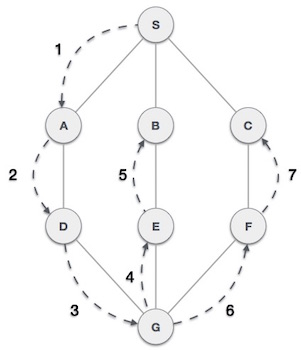
In the following graph, this algorithm traverses in a depth-ward motion and uses a stack to remember the next vertex to start a search, which is initiated once a dead-end occurs in any iteration. The path used to traverse the graph by DFS is from S to A to D to G to E to B first, then to F and lastly to C.
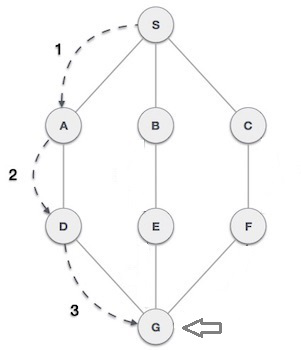
3.) Depth-Limited Search:
The third search algorithm, the depth-limited search (DLS) is similar to the depth-first search, with a minor difference that it has a predetermined limit. DLS is used to treat the depth limit node, as it does not have any successor nodes. DLS is best suited in cases where there is prior knowledge of the problem, which at times is difficult to achieve.
In short, this memory-efficient search algorithm is used to solve the drawbacks of the infinite path in the Depth-first search.
Example:
We can consider the example considered for Depth-First Search here too, as in DLS the only difference is that it has a set limit. Here, the algorithm will traverse in a depth-ward motion and uses a stack to remember the next vertex to start a search. But it will end the search when it reaches the limit, which in this case is G. The path used to traverse the graph by DLS is from S to A to D to G, which is the set limit.
4.) Iterative Deepening Depth-First Search:
A combination of DFS and BFS algorithms, Iterative Deepening Depth-First Search identifies the best depth limit, by gradually increasing the limit until the goal is achieved. Unlike the other two search algorithms, IDDFS is complete and is used to perform iterations of depth-limited searches while increasing the expected runtime. Moreover, if a solution exists, IDDFS will find a solution path with the fewest arcs.
This searching strategy is extremely beneficial, as it combines the benefits of both Breadth-First Search and Depth-First Search. The only drawback associated with this method is that it performs the search and work of previous stages.
5.) Bidirectional Search:
Extremely different from other search algorithms, the Bidirectional search executes two concurrent searches to find the final goal node, which is known as forward-search (Start State) and backward-search (Goal State). Bidirectional Search uses two small subgraphs, instead of one graph, wherein one starts the search from an initial vertex and other from goal vertex. It is only when these two vertices intersect that the search reaches its end. This algorithm has less time complexity and does not have high memory requirements.
It can be used in the following instances:
- When both initial & goal states are unique and completely defined.
- The branching factor is similar in both directions.
6.) Uniform Cost Search
Implemented through the priority queue, Uniform Cost Search is the best algorithm for a search problem, as it does not involve the use of heuristics. It gives maximum priority to the lowest cumulative cost and is equivalent to the Breadth-First Search algorithm in cases where the path cost of all edges is the same.
As this algorithm chooses the path with the least cost at every state, from start to goal, it can be used to solve any graph/tree that demands optimal cost.
Conclusion:
From the above discussion, we can conclude that the role of the Uninformed Search Algorithm is immense in the smooth functioning of AI machines and systems. This algorithm, along with the Informed Search Algorithm, enables the machines to perform assigned tasks accurately and reach its goal or result with utmost swiftness.
However, it is important to note that this discussion does not end here. As there is an entirely uncovered side of Search Algorithms, which will be covered in our next discussion on Informed Search Algorithms.