Anshul Jain
23 Mar 2020
Introduction:
Among the various components that are the foundation of Artificial Intelligence, Algorithms are at the top. It is a sequence of unambiguous instructions or specifications that are used to solve a problem, perform calculations, and conduct a sequence of specified actions. Artificial Intelligence is highly dependent on a range of algorithms, to perform evaluation function and to reach the goal state. Minimax Algorithm is one of these algorithms, which is used in decision making as well as game theory to find the most optimal move or solution.
But, what makes the Minimax Algorithm an integral part of Artificial Intelligence? What advantages does it offer?
To answer these questions and more, we are here with a detailed discussion on the Minimax algorithm AI, where we’ll define its importance, workings, advantages, and disadvantages, among other things.
So, let’s begin!
What is the Minimax Algorithm?
The Minimax Algorithm is a recursive or backtracking algorithm typically used in turn-based, two-player games. It is one of the most popular search algorithms used in AI for teaching AI Agents how to play strategy-based games. The popularity of Minimax is based on the fact that it takes into account all the possible moves that players can take at any given time during the game.
This enables the algorithm to minimize the opponent’s advantage while simultaneously maximize the agent’s advantage at every turn the AI gets to play.
However, to offer each player this advantage, minimax needs to know the suitable path in the search tree that leads to the goal state, which can only be achieved by traversing the tree to its terminal state and searching for all possible moves.
Minimax Algorithm Example:
Let us further understand the concept of the Minimax Algorithm, with the help of the following example:
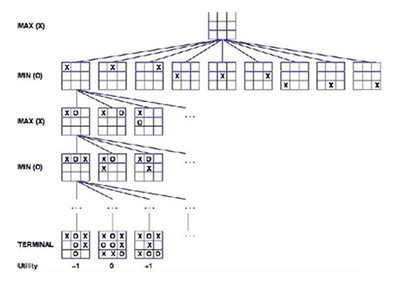
Here in the diagram, all the possible moves in the game of Tic Tac Toe are illustrated, each of which will be traversed by the minimax algorithm, using the depth-first algorithm. This process will continue until all the possible moves have been identified.
Properties of Minimax Algorithm:
Implemented using the depth-first search, the Minimax algorithm is suitable where the players have complete information about the game, as it is:
1. Complete:
Minimax is complete, as it definitely finds the solution (if existing) in the finite search tree.
2. Optimal:
It is optimal if both players play optimally.
3. Time Complexity:
The time complexity of the Minimax algorithm is O (bm), where b represents the game tree’s branching factor and m represents the maximum depth of the tree.
4. Space Complexity:
The space complexity of minimax is O (bm).
Workings of the Minimax Algorithm:
Applied to games like Checkers, Tic-Tac-Toe, Chess, etc., the Minimax Algorithm forms a tree-like structure through recursion, where the two players, Min and Max take the following steps to reach the final goal state of the game.
- Prepare the complete Game Tree.
- Evaluate the score of each branch, using the evaluation function.
- Back-up score from the nodes to the root by:
- Selecting the child node with a maximum score for Max player.
- Selecting the child node with the minimum score for Min player.
It is based on these values/scores that the quality (good or bad) of the move is decided.
- At the root node, the node with the max value is selected and the corresponding move is performed.
Throughout the process, the aim is to minimize the maximum loss or the worst case scenario and get the best solution for successful game playing.
Minimax Algorithm Advantages:
Minimax algorithm is a beneficial problem-solving algorithm that helps perform a thorough assessment of the search space. However, the most prominent advantage it offers is that it makes it possible to implement decision making in Artificial Intelligence, which has further given way to the development of new and smart machines, systems, and computers.
Minimax Algorithm Disadvantages:
While comprehending the Minimax Algorithm, it is imperative to highlight the various Minimax algorithm problems, as it enables us to look at both positive as well as negative sides of the algorithm. Hence, here are the disadvantages offered by the Minimax Algorithm:
- It has a huge branching factor, which makes the process of reaching the goal state slow.
- Search and evaluation of unnecessary nodes or branches of the game tree degrades the overall performance and efficiency of the engine.
- Both min and max players have lots of choices to decide from.
- Exploring the entire tree is not possible as there is a restriction of time and space.
Improving the Minimax Algorithm:
Though effective in finding accurate solutions in a simple game like Tic-Tac-Toe, the minimax algorithm is not the best choice for the games with exceptionally high branching factors. It is to improve this drawback, Alpha Beta Pruning is implemented in the Minimax Algorithm.
Alpha Beta Pruning seeks to decrease the number of nodes that are evaluated by the minimax algorithm, by passing two extra parameters Alpha and Beta.
Minimax Algorithm Implementation:
Minimax algorithm can be implemented with the help of the following pseudo-code. function minimax(node, depth, maximizingPlayer) is:
if depth 0 or node is a terminal node then
return static evaluation of node
if MaximizingPlayer then // for Maximizer Player
maxEva= -infinity
for each child of node do
eva= minimax(child, depth-1, false)
maxEva= max(maxEva,eva) //gives Maximum of the values
Return state= maxEva
else // for Minimizer player
minEva= +infinity
for each child of node do
eva= minimax(child, depth-1, true)
minEva= min(minEva, eva) //gives minimum of the values
return min Eva
Conclusion:
Minimax Algorithm is one of the beneficial algorithms that have allowed researchers to traverse into new fields of smart and intelligent machines, that are capable of playing and winning games like tic-tac-toe, chess, checkers, Go, etc. against human opponents. Though not untouched by drawbacks, Minimax still remains an effective search algorithm whose advantages are further improved with the help of the Alpha Beta Algorithm.
To learn about Minimax Algorithm neural networks, look out for our next article.