Alpha Beta Pruning AI

Introduction to Alpha Beta Pruning AI:

Also known as Alpha Beta pruning algorithm, Alpha Beta Pruning is a search algorithm that is used to decrease the number of nodes or branches that are evaluated by the Minimax Algorithm in the search tree. It is termed as the modified version as well as the optimization technique for the minimax search algorithm and is used commonly in machines playing two players games like Go, Tic Tac Toe, Chess, etc.

Alpha-Beta Pruning is known so because, it passes two additional parameters in the minimax function, namely Alpha and Beta, that represents the best value that the maximizer guarantees as well as the best value that the minimizer guarantees at that level. Also, the Alpha here is negative infinity and beta positive infinity, and players start the search with their worst possible score.

This algorithm is extremely beneficial, as it reduces the computation time and makes the search go deeper in the game tree, quickly. Moreover, Alpha Beta cutoff or prunes the evaluation in the game tree, when even a single possibility is found that proves the current move is worse than the previously examined move.

Alpha Beta Pruning algorithm example:

Let us consider one of the two-player games we mentioned earlier for this example, Tic Tac Toe, wherein each opponent has to pick a symbol (X or O) to represent them on a 3 by 3 board. The objective here is to reach the final game state, which is greater than or equal to (≥) the child node evaluated before it. The evaluation function is initiated by generating the entire game tree and performing the evaluation function until the Alpha Beta Pruning condition is achieved.

The idea, in short, is to search for all possible moves, by simultaneously pruning the areas that do not require further searching.

How do you implement Alpha Beta Pruning in Minimax?

Before we discuss the implementation of Alpha-Beta Pruning in the Minimax algorithm, let us get an insight into the concepts of the latter.

Minimax, which is also known as MinMax, MM, or saddle point, is a backtracking algorithm, used in decision making, statistics, as well as game theory to find the most optimal move for a player and to minimize the possible loss for a worst-case scenario. Unlike Alpha-Beta Pruning, this algorithm tries to see every possible outcome and then tries to optimize the final option it has in hand. Hence, it is termed as a two-pass search, wherein one pass is used to assign heuristic values to the nodes, while the other is responsible for propagating them up the tree.

Implementing Alpha Beta Pruning in Minimax:

This tree consists of various layers of min and max values, which represent the two parameters Alpha value (- ∞) and the beta value (+∞).

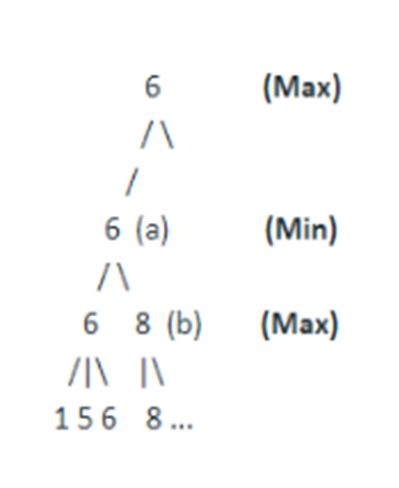
Each node respectively represents the minimum score that the maximizing player is assured of and the maximum score that the minimizing player is assured. Therefore, the search here is initiated from the player max and is continued to other branching factors. It was only after reaching the leaf node with a similar value of 8 that the search was terminated, as the algorithm does not consider searching further necessary.

This search would have been continued to its last node, had we implemented just the minimax algorithm, which as stated earlier tries to assess all possible outcomes and then optimizes them to reach the final goal.

Workings of Alpha Beta Pruning:

Performed with an aim to reach the goal state effectively and swiftly, Alpha-Beta Pruning involves an intuitive process, which is initiated by setting variables alpha and beta to the worst-case values. This process further involves four important steps which are:

• Initiate the search, down the tree, to the given depth.
• After reaching the bottom, determine the utilities of the higher nodes, using the utilities of the terminal nodes.
• Based on the branching factors of whether the move backtracked was made by the opponent or the computer, backtrack, propagate the values and path.
• Finally, when the search is complete, the Alpha value at the top node gives the maximum score that the player is guaranteed to score.

Move Order of Alpha-Beta Pruning:

Another important aspect that we need to consider while comprehending the workings of the alpha-beta algorithm is its move order, as its effectiveness is highly dependent on the order in which each node is examined. These are of two types:

• Worst Ordering: At times, the algorithm works similar to the minimax algorithm, without pruning any branches of the search tree. This is known as the worst ordering, where the alpha-beta pruning time complexity is higher.
• Ideal Ordering: In this move order, excessive pruning happens in the search tree and best moves occur at the left side of the tree.

Alpha Beta Pruning Pseudo Code::

function minimax (node, depth, isMaximizingPlayer, alpha, beta):
if node is a leaf node:
return value of the node

if MaximizingPlayer:
maxValue = -INFINITY
for each child node:

value = minimax(node, depth+1, false, alpha, beta)
maxValue = max( maxValue, value)
alpha = max( alpha, bestVal)
if beta <= alpha:
cut off
return maxValue

else :
minValues = +INFINITY
for each min nodes:
value = minimax(node, depth+1, true, alpha, beta)
minValues = min( minValues, value)
beta = min(beta, minValue)
if beta <= alpha:
cut off
return minValue